音響心理学とは
音響心理学とは人間の聴覚に関する学問であり、物理学、音響学、心理学、生理学、認知、知覚、音楽理論など様々な分野の研究成果の組み合わせで成り立っています。古来から作曲家、演奏家、指揮者は経験的に音響心理学の分野の研究成果のようなものを知っていますが、それらを体系的に学習し、自身の音楽表現に反映させることは表現者と聴衆の距離を縮めるためには欠かせません。このページではMax/MSPのプログラミングを通じていくつかの音響心理学の法則や規則を紹介します。
また、音響心理学の実験を行う際にもMax/MSPによるプログラミングは大変有効です。CやJavaで書けば大掛かりになってしまうプログラムもMaxを利用すればシンプルに記述できるため、クリエイターだけでなく音響心理学、音楽心理学、音響学を専門にされているかたにもおすすめします。
耳の働き
我々の耳の役割は、外部の気圧の変化を神経パルスに変換し、脳へ信号を送ることです。
人間は生まれたときから成人とほぼ変わらない音の知覚をする能力がありますが、その情報を脳で解釈し、認知するには発育が必要となります。認知の能力を伸ばすのには臨界期があり、幼少期に十分な音の入力が行えない状態で育った人間には認知能力が欠如してしまい、大人になってから経験を積んでも入力されてくる音を解釈する脳のメカニズムを十分に形成することができなくなってしまいます。このことからも、我々の聴覚の効率的な発達のためには幼少期の音響体験が非常に重要になってきます。
耳の構造
人間の耳は大きく分けて外耳、中耳、内耳の器官に分類することができます。

外耳 (Outer ear)
外耳には耳殻 (external pinna)、外耳道 (auditory canal)があり、耳殻は外部の音を集音する効果と高い周波数に対してその音がどの方向から発せられているのかを測定する機能があります。外耳が音の方向性を測定する機能は、周波数によって異なります。これは低い周波数ほど波長が長く、高い周波数ほど波長が短いという原理に基づいています。
日光が差しているときに、太陽の位置、角度によって物体には影ができます。これと同様に、音にも影のようなものがあります。この音響の影を知覚する際に我々の左右両方の耳が必要となります。人間の二つの耳は左右に配置されており、例えば右側から鳴った音は左耳よりも右耳に早く到達します。そして、到達時の位相が異なります。この差を脳内で計算し、我々はどの方向から音が鳴っているのかを認識します。試しに、耳を手で折り畳むと音が聞こえる方向が変化して聞こえることがわかると思います。
我々の耳が左右の方向よりも上下の方向感覚に弱い理由は両耳が左右平行についていることが原因です。また、前後方向の距離感は音量の大小で判別を行っています。
もう一つの器官である、外耳道はレゾネーターの役割を果たします。2000Hzから5000Hzの周波数帯域の音をブーストし、中耳へ振動を伝達します。
中耳
中耳は鼓膜から先の器官です。鼓膜 (Ear drum)は槌骨(Malleus)、砧骨(Incus)、鐙骨(Stapes)という3つの小さな骨と接続されています。太鼓の膜のような鼓膜が空気の振動をとらえ、中耳骨が機械的な振動に変換し、内耳に送り出す機能があります。中耳骨は音を聞くプロセスの中では重要な器官であり、とても小さな音圧でも30倍程度まで信号を増幅し、内耳に伝えることが可能です。反対に大きすぎるノイズや突発的な圧力の変化を軽減する機能も備えています。
内耳
内耳は耳の元も奥深い位置の器官であり、液体で満たされています。平衡感覚を司る三半規管などが内耳には含まれますが、聴覚と直接関係があるのは蝸牛(Cochlea)です。卵円窓という小さな穴を通じて中耳から信号を受け取ります。内部は1万ほどの有毛細胞があり、周波数分析をしています。例えば、1600Hzの音は入り口から20mmほどの細胞が発火し、200Hzは30mmの位置、50Hzは35mmの位置の細胞が発火することがわかっています。(Georg von Bekesy 1960.)
Fletcher-Munson ラウドネス曲線
人間の耳には全ての周波数の音が均一に知覚されるわけではなく、ある周波数では他の周波数より音が大きく知覚されたり、小さく知覚されたりすることがあります。 この特性を扱った図が、フレッチャーマンソンの等ラウドネス曲線と呼ばれるものです。
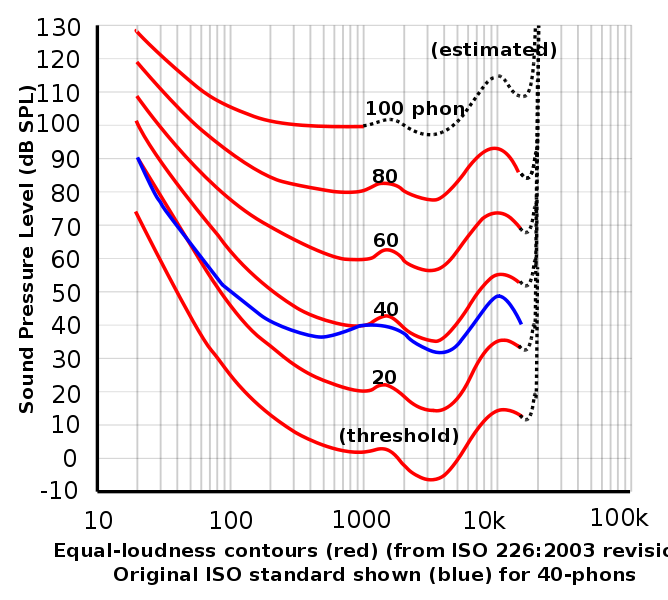
この図で描かれている赤と青の曲線は同じ音量と知覚される音圧レベルを結んだ曲線です。例えば1000Hzで60dBの音と同じ大きさを100Hzで感じるようにするためには約80dBの音圧レベルが必要となります。この図からもわかるように、我々が全ての周波数を同じ音量に知覚できるようにするにはこの曲線に従って音の大きさを決定する必要が生じます。
これはレコーディングにおけるミキシングの際にもVUメータやフリークエンシーアナライザーで同じだけレベルメータが動いているのに、周波数によっては音が奥に引っ込んで聞こえる際にも有効な理論であり、オーケストレーションも含め、複数の音を組み合せて総合的な音響を組み立てる際に重要になってくる考え方です。
phon ホン
1000Hzにおける純音(サイン波)の音圧レベル(dB)をホンという単位で表すことができる。音圧レベルとホンの関係は上の曲線に示してある通りです。例えば40ホンは1000Hzで40dBであり、100Hzでは約60dBの音圧レベルを示す曲線となります。
等ラウドネス曲線を知覚する実験
以下のyoutubeコンテンツは等ラウドネス曲線を耳で体感していただくための映像です。同じ音量で録音を行っているのでレベルメータにもその様子が表れていると思いますが、我々の耳には周波数によって音量が異なって聞こえることがわかると思います。
Max/MSPパッチのダウンロード
Fletcher-Munson.maxpat.zip (for Max5)
max5Runtime(上記のMaxパッチの実行用フリーソフトウェア for Mac)
max5Runtime(上記のMaxパッチの実行用フリーソフトウェア for win)
臨界帯域
二つの純音の周波数がとても近い場合、我々は通常とは異なる音響現象を耳にします。これは周波数、音色、音量にかかわる現象であり、まず音の大きさが2つの純音の和よりも小さくなることが確認できると思います。この通常ではない音量の和は一定の周波数差まで続き、ある領域を抜ける純粋に二つの別々の純音の音量の和を知覚できることができると思います。この周波数の差のことを臨界帯域(critical band)と言います。
臨界帯域内では二つの純音はその周波数の差分のうなりを伴います。この効果は丁度トレモロのように知覚されるでしょう。20Hz以上の差となると、うなりというより、全く別の周波数となって二つの純音が聞こえてきます。これは我々の不協和に関する知覚に重要な役割をはたします。
臨界帯域を確認する実験
2つの純音(サイン波)を発生させるオブジェクトを用意し、一方の周波数を固定、もう一方の周波数を可変させています。どの程度の差から我々は2つの音を別個の音だと知覚できるようになるか、耳で確かめてください。臨界帯域は周波数によって異なる幅を持ちます。
Max/MSPパッチのダウンロード
Critical bandwidth.maxpat.zip (for Max5)
max5Runtime(上記のMaxパッチの実行用フリーソフトウェア for Mac)
max5Runtime(上記のMaxパッチの実行用フリーソフトウェア for win)
Sound Localization サウンドローカリゼーション
我々人間は音の発音源としての口は1つありますが、集音源として2つの耳があり両耳が音響現象の解釈に様々な役割を果たしています。
一つは音源の位置を特定する能力です。ある音源から両耳に音が届くとき、音源の位置が右に寄っていれば右耳と左耳での音の到達時刻に差が生じます。到達時間が異なるという事は、耳に届いた時点での音源の位相にも差が生じるということです。この時間差と位相差などを利用し人間は音源のローカリゼーションを行っています。
低い周波数ほどローカリゼーションは曖昧になる
Lord Rayleighは1876年の実験で人間のローカリゼーション能力は周波数によって決まることを突き止めました。彼は、低い周波数で我々のローカリゼーション能力が低いことを発見し、それはsound shadow(音の影)によるものだと説明しています。
以下の映像でも我々の耳は低い周波数になるほど左右の音源の位置特定が曖昧になることがわかると思います。
位相差を用いた実験
1907年にRayleighは位相差を使って、音源のローカリゼーションを行う実験をしました。
位相を考える際には音源の波長を考えなければなりません。波長は周波数が低いほど長く、高いほど短いということが物理学によって説明できます。つまり、位相差は周波数が高いほど大きく生じることになります。
このことから同じ周波数でも位相差をコントロールする事で擬似的に音源が移動しているように聞かせる事が可能なのではないかという仮説が成り立つと思います。以下の映像は同じ周波数を持つ二つの音源の一方の位相を周期的にコントロールしている例です。左右両方のチャンネルの出力は変化していないにも関わらず、我々の聴覚には左右の音量が変化しているように感じるでしょう。ローカリゼーションには位相が大きく関わっていることが推測されます。
ローカリゼーションに使用したMaxパッチのダウンロード
Rayleigh second theory.maxpat.zip
Localization.maxpat.zip
max5Runtime(上記のMaxパッチの実行用フリーソフトウェア for Mac)
max5Runtime(上記のMaxパッチの実行用フリーソフトウェア for win)
ゲシュタルト心理学と音の錯覚

人間がある形を知覚する際、物体と背景の関係をまず認識します。我々の脳内で、例えばグランドに転がる野球のボールは、土という背景とボールという物体の2つを分類して解釈します。
この物体と背景の関係を説明する上で良い例が左のルビンの盃です。この絵は「互いに向かい合ってる人間の顔」と、「盃」の2つを内包した両義図形です。 白い部分と黒い部分のどちらを物体、どちらを背景ととらえるかで異なった意味を持ちます。そしてその2つの意味は同時に解釈されることはなく、我々の脳はどちらか一方の見方しか同時にとらえることができません。
我々が物体を知覚する場合、それが背景に対して物体であると認識するにはいくつかの条件が必要となります。
その条件はゲシュタルト心理学によって明らかにされていますが、音楽においても幾つかの音をグループとして知覚する際にゲシュタルト法則と同じような分類を行うことが明らかになってきています。
連続の法則
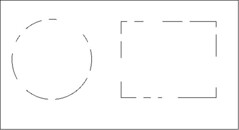
人間は輪郭でまとまった物を物体として認識することができます。右の例のように直線や円形が欠けていたり、ある物体で隠されている場合でも円形や直線など数学的に連続性を持つ形であれば読み取ることができます。その輪郭に足りない部分はある程度脳内で補完する能力が我々には備わっています。
音楽においても連続の法則は有効で、下の実験音声を聞くとそれぞれが別個のものではなく、一つのグループとして知覚されていることがわかると思います。
無音によってカットされた音声
ホワイトノイズによってカットされた音声
これら2つの音声を聞き比べると、ホワイトノイズによってカットされた音声のほうが我々には聞き取りやすいことがわかると思います。これは、ホワイトノイズにはすべての周波数成分が含まれており、我々の脳内で足りない音を補完する際に一種のフィルタリングのような処理を行っているからだと考えられます。無音によってカットされた音声のほうは、何も無い中から脳内で情報を補完するため、フィルタリングよりも不正確であることが予想されます。
近接の法則

ある点と点が近接している場合、我々はそれらにまとまりを感じグルーピングを行います。これが近接の法則です。
図の右側の円からは3つのグループを感じることができるでしょう。これは円同士が近接しているものをまとめて一つのグループとして知覚するからです。
音楽の場合でも近接の法則に似た現象があります。我々が旋律を知覚するときには、ある音と次の音の音程が近接しているほど線的な進行を感じます。更にこれはスピードが上がるほど顕著になります。この現象をKorte’s third lawと呼びます。下の映像では長二度の音程の進行を繰り返したの場合、我々の耳には旋律として知覚されますがもっと広い音程関係にある完全五度の進行を繰り返した場合、一定のスピードを超えるともはやその繰り返しは旋律ではなく別個の音が同時に鳴っているように聞こえます。
Korte’s third law
Max/MSPパッチのダウンロード
Korte.maxpat.zip (for Max5)
max5Runtime(上記のMaxパッチの実行用フリーソフトウェア for Mac)
max5Runtime(上記のMaxパッチの実行用フリーソフトウェア for win)
類同の法則

同じような特徴を持った物体が一つのグループを形成しやすいことを類同の法則と呼びます。右の図では横並びの白い物体と黒い物体が別々のグループを形成していることを感じると思います。これを縦並びで白、黒、白、黒、白というグループとして知覚する人は少ないと思います。
これは色だけでなく、形の類似性にも当てはまります。同じ形をしたものであれば大小は違えど同じグループを形成しやすいという特徴があります。
音楽の場合の類同の法則は音色が考えられます。
同じ音色のものは一つのグループを形成しやすいことから、作曲家は古くからオーケストレーションなどでこの法則を応用してきました。仮にオーケストラの全ての楽器が同じ音色であったとしたら、我々は細かい声部の違いを聞き分けることができず、音楽から多彩な進行を感じることができなくなってしまうでしょう。
音響心理学の参考文献
コンピュータ音楽―歴史・テクノロジー・アート
|
|
 |
コンピュータミュージックジャーナルの責任者であったCurtis Roads氏のComputer Musicの翻訳版。コンピュータ音楽―歴史・テクノロジー・アート |
Science of Sound, The (3rd Edition)
|
|
 |
音響心理学の授業でよく教科書にしていされる本です。 |
Music, Cognition, and Computerized Sound: An Introduction to Psychoacoustics
|
|
 |
プリンストン大学のPerry R. Cook 氏が書かれた音楽認知に関する有名な教科書です。付録のCDには様々な音響実験のサンプル音源が含まれており、教科書と合わせて聞くと理解が深まる。 |