カオス理論とは
カオス理論とは、決定論的で動的なシステムの一部に見られる、予測できない複雑な様子を示す現象を扱う理論です。値の振る舞いは決定論的法則に従うものの、その過去および未来の振る舞いの予測には、初期値など無限の精度の情報が必要とされるため、観測による予測が不可能に近いものをカオスといいます。
1960年代に、ある非常に簡単な数式が滝の水しぶきのような複雑な自然界の動きをモデリングすることが発見され、カオス理論に注目が集まるようになりました。
一般的にカオス理論はアメリカが発祥と思われていますが、実際にはこれに先駆けて日本の京都大学工学部の上田睆亮が1961年に既にカオスの基本的な性質を発表しています。
カオス理論を音楽の作曲に活かす動きは90年代のコンピュータ音楽界で流行し、中にはオウテカなどポピュラー音楽のミュージシャンでもこの理論を使い作曲を行う例があります。
3種類の特徴的振る舞い
- 1つの安定した値に収束する領域
- 周期的な振る舞いを見せる領域
- 周期性や収束が見られない振る舞いを見せる領域
その他の特徴
- 単純な数式から、複雑な数列を生成する(ランダムではなく決定的)
- ミクロで観測すると秩序があり予測可能な箇所がある
- 初期値のわずかな違いが未来の状態に大きな違いをもたらす初期値鋭敏制がある
- 自己相似性
カオス理論の音楽への応用
複雑系のような非線形の振る舞いを見せるシステムのコンピュータ音楽への応用は1980年代あたりから多くの作曲家や研究者に試みられてきました。その範囲は音響合成からアルゴリズム作曲まで多岐に渡ります。
このようなシステムはデータの初期状態に依存して幾つかの異なるタイプの結果を出力する特徴があります。
1988年にMITのJeff Pressingはカオスが持つ非線形軌道を音楽のパラメータに利用するために、4次方程式を利用した自動作曲を行っています。マップの出力はピッチ、デュレーション、エンヴェロープ、ダイナミクス、テクスチャーの密度、タイミングなどに適用されました。実際の楽譜の一部は以下の文献で見る事が可能です。
その他の例では、Fred LerdahlとRay JackendoffのGTTMのツリー構造をカオス理論の軌道を元に生成したJeremy LeachとJohn Fitchの1995年のシステムがあります。
 |
Algorithmic Composition: Paradigms of Automated Music Generation Springer 2008-12-12 |
LogisticMap / ロジスティックマップ
Logistic Mapは1976年にR.Mayが発見したカオス生成関数です。この関数は以下の式のように非常に簡単な数式として定義が可能なものです。
Xn+1 = λ * Xn * (1 - n) (0 < λ <= 4)
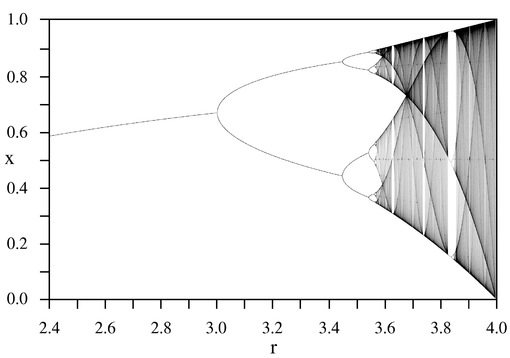
この式は一つ前の値が次に生成される値に影響を与える式となります。λの値によってその振る舞いはダイナミックに変化します。例えばλの値が0から1の場合は0に収束し、1から3の場合は1 – 1 / λに収束、3以上では2点間を反発し合うゆな振る舞いになります。
そしてλが3.449449の場合周期が2点ではなく4点になり、その後それは8周期となり、乱気流のように複雑な振る舞いへと成長していきます。これは分布だけでなく、値のシーケンス自体もどこか周期的な振る舞いが見られ、単なるループではないけれど関連性を感じる数値のグルーピングを行う事すら可能な振る舞いを見せます。
これは音楽のモチーフが変形している状態に酷似しているため、応用例が多いλ値です。サンプルのyoutube映像では旋律の生成にlogisticMap.javaを利用していますが、現代のアルゴリズミックコンポジションではこのようなアプローチはありきたりの常套句となり、波形の生成、音色、楽式など楽曲の高次構造、オーケストレーション、リズムの生成などもっと様々なパラメータに応用する研究が進んでいます。
Max/MSPでのカオス理論の利用
Max/MSPにおいてカオス理論を応用するにはJSかMXJを利用するのが最も手軽です。Maxのパッチングだけでこのような数式を実行するには可読性や作業効率の面でデメリットが目立つため今回はMXJのためのソースコードを紹介します。
このコードをコンパイルし、mxjオブジェクトのアーギュメントとしてクラス名を書けばすぐさまmaxのオブジェクトとして機能します。
注意したいのは、これらは単なる数式です。この材料をどう創作に活かすかが作曲家の腕の見せ所になります。楽器だけ与えられても優れた曲が書けるのとは限らないのと同様、これらのオブジェクトもあくまで材料であって、それを使うだけで創造性が保証されるようなものではありません。
90年代のコンピュータ音楽の世界でもカオスというだけで創造的なイメージがありましたが、あまりに多くの作曲家がカオス理論を応用した作品に走ったため、現在では本当に音楽的に有効な使い方でない限り、時代遅れのツールという印象すら持たれる危険性はあります。
logisticMap.java
import com.cycling74.max.*;
public class logisticMap extends MaxObject {
float x=0.5f;
float lambda=3.00f;
float y;
public logisticMap(Atom[] args) {
declareAttribute("lambda");
}
public void bang() {
y = lambda * x * (1-x);
outlet(0, y);
x=y;
}
}
dowonload
Tinkerbell Map
package m;
import com.cycling74.max.*;
public class tinkerbellMap extends MaxObject {
double x_1 =0.1;
double y_1 =0.1;
double x_2;
double y_2;
double a=0.9;
double b=-0.6013;
double c=2;
double d=0.5;
//a=0.9, b=-0.6013, c=2, d=0.5.
//a=0.3, b=0.6, c=2, d=0.27.
public tinkerbellMap(Atom[] args) {
declareAttribute("a");
declareAttribute("b");
declareAttribute("c");
declareAttribute("d");
}
public void bang() {
x_2 = (Math.pow(x_1,2)-Math.pow(y_1,2))+a*x_1 + b*y_1;
y_2 = 2* x_1 * y_1 + c*x_1 + d*y_1;
outlet(0, x_2);
outlet(1, y_2);
x_1 =x_2;
y_1 =y_2;
}
}
Gingerbreadman Map
package m;
import com.cycling74.max.*;
public class gingerbreadmanMap extends MaxObject {
float x_0 =0.7f;
float y_0 =1.3f;
float x_1;
float y_1;
float seed =0.92f;
public gingerbreadmanMap(Atom[] args) {
declareAttribute("seed");
}
public void bang() {
x_1= (float)(1- y_0- (Math.abs(x_0)* seed));
y_1= x_0;
outlet(0, x_1);
outlet(1, y_1);
x_0= x_1;
y_0= y_1;
}
}
Clifford Attractor
package m;
import com.cycling74.max.*;
public class cliffordAttractor extends MaxObject {
float x_0 =0f;
float y_0 =0f;
float x_1;
float y_1;
float a=-1.4f;
float b=1.6f;
float c=1.0f;
float d=0.7f;
public cliffordAttractor(Atom[] args) {
declareAttribute("a");
declareAttribute("b");
declareAttribute("c");
declareAttribute("d");
}
public void bang() {
x_1 = (float)(Math.sin(a*y_0) +c*Math.cos(a*x_0));
y_1 = (float)(Math.sin(b*x_0) +d*Math.cos(b*y_0));
outlet(0, (x_1+2) /4);
outlet(1, (y_1+2) /4);
x_0 =x_1;
y_0 =y_1;
}
}
Bakers Map
package m;
import com.cycling74.max.*;
public class bakersMap extends MaxObject {
double x=0.5d;
double y=0.5d;
double x_2;
double y_2;
float a =0.4999f;
float b =0.59f;
float c =0.21f;
public bakersMap(Atom[] args) {
declareAttribute("a");
declareAttribute("b");
declareAttribute("c");
}
public void bang() {
if(y < a){
x_2 = b*x;
y_2 = y/a;
}
else{
x_2 = (1-c)+c*x;
y_2 = (y-a)/(1-a);
}
outlet(0, x_2);
outlet(1, y_2);
x =x_2;
y =y_2;
}
}
Henon Map
package m;
import com.cycling74.max.*;
public class henonMap extends MaxObject {
float x_1 =0f;
float y_1 =0f;
float x_2;
float y_2;
float a =1.4f;
float b =0.3f;
public henonMap(Atom[] args) {
declareAttribute("a");
declareAttribute("b");
}
public void bang() {
x_2 = 1 -(a * x_1 * x_1)+y_1;
y_2 = b*x_1;
outlet(0, x_2);
outlet(1, y_2);
x_1 =x_2;
y_1 =y_2;
}
}
カオスを利用したシンセサイザー
これまでの例はあくまで数値としてカオスの特性を出力するためのアルゴリズムを提示しましたが、それをそのままMax/MSPのリアルタイム音響合成に活用すればシンセサイザーを作ることができます。
カオスの非線形性を利用したMac OSX用のシンセサイザーは以下の二種類があります。いわゆる平均律のドレミの周波数の周期的な波形が発音されるのではなく、周期性と非周期性、つまり楽音とノイズの間をパラメーターで行ったり来たりで切るシンセサイザーです。
Logistic Map
http://akihikomatsumoto.com/download/logisticmap.html
Henon Map
https://gumroad.com/l/SchM