
音楽、音響プログラミングにおける数学
音楽や音響、その他グラフィックのプログラミング学習において数学は不可欠となります。現状の日本の音楽大学、美術大学、芸術大学のカリキュラムの特性上、入試に数学は課されないケースが多く、高校レベルの最低限の基礎力すら身に付けずに大学での勉強を開始することが可能なため、多くの学生が数学の壁に突き当たります。このページはメディアアートのプログラミングの勉強、文献を読み解く上で最低限必要な数学のルールをいくつか紹介します。
Sets (集合)
sets(集合)とはelements(要素)の集まりです。現代の数学において集合論は非常に重要な概念で、ほとんどの理論が集合論を利用しています。この場合要素の順序自体は問題ではなく、複数の同じ要素が集合の中で重複していないことが前提となります。
集合の例
setA = {C,E,G}
setB
= {0,2,4,5,7,9,11}
setC
= {Do, Re, Mi, Fa, Sol, La, Si}
E ∈ setC
5 ∈ setB
∈の記号はEという要素がsetCという集合に含まれることを意味します。
空要素の場合
集合の要素が空の場合、その集合はnull setという言葉で示し、∅ か { }の記号で要素が空であることを表します。
普遍集合の場合
全ての集合、要素を含む普遍的な集合のことを普遍集合(universal set)と呼びます。Eという記号を使うことが多いです。
集合を図示する方法
普遍集合は長方形のダイアグラムで示す事ができ、集合は円で図示することが一般的です。
Subsets (部分集合)
A ⊆ B という式がある場合、AはBの部分集合(subset)であるという意味になります。これはAの全ての要素がBの要素でもあることを意味します。 そしてこの場合のBの集合を上位集合(superset)と呼びます。
部分集合の例

A = {1, 2, 3}, B = {1, 2, 3, 4, 5}
∴ A
⊆ B
もし A ⊆ B かつ B ⊆ Aが成り立つ場合、AとBは等しいことになりますA = B。
A ⊂ Bという記号がある場合、AはBの部分集合であると同時に、A = Bが成立しないということを意味します。
Complements (補集合)
A′の記号はAの補集合を意味します。補集合とは普遍集合から部分集合を除いた要素全てを意味します。
補集合の例
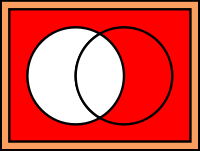
普遍集合 = E
部分集合A
= {x | x > 5}
このとき補集合 A′は{1, 2, 3, 4, 5}
Intersections (共通集合)
A ∩ Bという記号は集合Aと集合Bの共通集合を意味します。これはAにもBにも含まれる要素が含まれていることを示します。
共通集合の例

{1, 2} ∩ {red, white} = ∅
{1, 2} ∩ {1, 3, 5} = {1}
{1, 2} ∩ {1, 2} = {1, 2}
Unions (和集合)
和集合とは複数の集合を繋ぎ合わせたものです。A ∪ Bは集合Aと集合Bの結合を意味します。要素はAかBに含まれるもの、もしくは、AにもBにも含まれるものとなります。
和集合の例
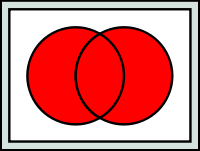
{0, 2} ∪ {4, 7} = {0, 2, 4, 7}
{1, 2, a} ∪ {x, y, a} = {1, 2, x, y, a}
{1, 2} ∪ {1, 2} = {1, 2}.